Special Relativity and Endurantism
Alexander R. Pruss
Abstract
According to endurantists, an object wholly exists at every time at which it is present. Hales and Johnson (2003) have argued that endurantism is incompatible with Special Relativity. Their argument, however, is logically invalid. One can make the argument valid by restricting its conclusion, but the problem that this argument poses to endurantism can be handled and is little more than a combination of two non-relativistic problems: Lewis’s problem of temporary intrinsics and Merrick’s problem of replaceable parts. Nonetheless, we shall see that endurantism conjoined with Special Relativity does yield some counterintuitive consequences.
Word count including title and notes, but not including abstract: exactly 4000 words.
1. Introduction
Endurantists believe that spatially extended physical objects are three-dimensional entities that wholly exist at different times. Perdurantists, on the other hand, believe that spatially extended physical objects are four-dimensional entities, and exist at a time only in by virtue of a time-slice wholly existing at that time. The familiar three-dimensional things around are such slices of four-dimensional worms. Common sense, of course, stands behind endurantism. On the other hand, the main philosophical argument for perdurantism is David Lewis’ problem of temporary intrinsics.[1] If a lump of clay is a ball at one time and a cube at another, then it seems that the lump is both wholly a ball, as it wholly exists at a time at which it is a ball, and likewise wholly a cube. This appears absurd. Being a ball and being a cube are intrinsic properties, and nothing can have both.
Recently, Hales and Johnson[2] have argued that Special Relativity (SR) presents a particular difficulty for the endurantist. We shall see, however, that Hales and Johnson’s argument for this is simply invalid. I will then consider an interesting improvement on Hales and Johnson’s argument, and argue that even with that improvement, we do not have a special problem with SR—the difficulty reduces to difficulties that non-relativistic non-presentist endurantists face, such as the problem of temporary intrinsics, and all the solutions to those problems can be used to avert contradiction here. Here, I will argue that we will need to realize that given Special Relativity, the “times” referred to in non-relativistic endurantism need to be replaced by space-like hyperplanes.
I will then note two interesting consequences of relativistic endurantism. The first is that it follows that extended objects self-intersect. This strangeness raises the price of endurantism. The second is that it becomes highly plausible that bilocation—an object’s wholly existing in more than one place at a time—is possible. Whether this raises the price of endurantism is unclear. After all, time travel to a time at which one had existed implies bilocation[3], and time travel appears conceivable to many. And in any case we already knew that relativity theory was both true and strange.
2. The Hales and Johnson argument
Consider an object o at a time t, in o’s rest frame, and suppose this frame is inertial. If endurantism is true, then all of the object’s parts exist at t, since an object is wholly present at a time if and only if all of its parts exist at that time. But now consider a reference frame F moving with respect to o. In that reference frame, o has proper parts. Since simultaneity in F does not coincide with simultaneity in o’s rest frame, some of these proper parts of o will exist at t and some prior to and/or after t. Therefore, o has proper parts at times other than t. “Thus every object has proper parts at different times” and, Hales and Johnson claim, it follows that “no object wholly exists at each moment of its existence”. For if an object wholly exists at every time at which it exists, as endurantists claim, then “at every time t at which o exists, every proper part of o is at t” (p. 535).
The argument needs to be restricted to apply to physical objects that (a) have proper parts (unlike elementary particles) and (b) where these parts are not all co-located. For convenience, I will call such objects “extended”, though the term is somewhat unhappy.
Even thus restricted, the argument is still invalid. For the argument depends on an inference from:
(1) Every extended object has proper parts at different times
to
(2) No extended object has all of its proper parts at any one time.
This inference is not logically valid, since one cannot conclude from “Every A has Bs at different Cs” that “No A has all of its Bs at one C”, without an auxiliary premise prohibiting a B from existing at more than one C.
Thus, the inference from (1) to (2) appears to require the auxiliary assumption:
(3) If a proper part of an extended object exists at a time other than t, then that proper part does not exist at t.
Otherwise, it is quite possible for an object to have proper parts at times other than t and yet to have all of its proper parts at t, namely if those proper parts that it has at times other than t are also proper parts of it at t.
But it should now be clear that (3) will be rejected by every endurantist who believes in extended objects, since according to endurantism just as objects like dogs exist at more than one time, so do their proper parts like hearts and tails. The only endurantist who will accept (3) will be an endurantist who rejects the existence of extended objects and who takes (3) to be trivial. The argument amended with the addition of (3) begs the question against endurantists who believe in extended objects.
Note that Kristie Miller[4] has criticized Hales and Johnson for assuming that co-existence is transitive. However, while Hales and Johnson’s less formal account of their argument does talk about co-existence, their formal summary does not. Their formal statement makes it clear, too, that an endurantist has no need to talk about co-existence—all she needs to talk about is existence at a time. The less formal account also discusses cases where the part as found at a different time has some different property, e.g., it is exploded. But, again, the endurantist accepts the idea of objects having different properties at different times.
3. Changing assortments of parts
There is, however, a way of restricting the conclusions of the Hale and Johnson argument that escapes the above difficulty. Consider a cat that loses its tail. Suppose we are located at a position x in the skull of the cat at a time t (that requires us to be very small), and are looking at the situation from the cat skull’s rest frame R (assume the cat doesn’t move, so this frame is inertial). Assume that the tail is instantaneously destroyed at t0 in our reference frame. Endurantists who believe in extended objects should have no problem accepting this possibility. Suppose that t0 was very shortly before t, so much so that t-t0 is smaller than the amount of time it takes light to travel from the closest end of the tail to us.
Then by the relativity of simultaneity it turns out there is a reference frame F such that relative to F it is true at <x,t> that the destruction of the tail has not yet taken place. This will be a frame that is moving at a near-light velocity in the direction pointing from the head to the tail. Then relative to F, we (who, remember, are at x) could correctly say at t: “The tail (still) exists.” But relative to R, it would be correct for us to say instead at t: “There is no tail.” It seems, thus, that in R it is false that the cat wholly exists at t. For, relative to R, not every part of the cat exists at t, since the tail does not exist at t. Therefore, it seems that endurantism cannot hold relative to R. This is the Relativistic Loss Argument (RLA).
But now observe that this argument seems unduly complex. We can remove all considerations of SR, and give the following simpler Non-Relativistic Loss Argument (NRLA): “Suppose a cat’s tail is destroyed at t0 and the cat survives that loss. Then, the endurantist is committed to the claim that the cat wholly exists after t0, since it survives the loss. But one of the cat’s proper parts, namely the tail, fails to exist after t0. Hence, endurantism is false.” This argument has, in essence, been given by Trenton Merricks[5] who held that presentism was the only possible answer for an endurantist—according to presentism only present things and events are real. Since presentism entails a privileged reference frame—namely the frame defined by treating all the real events as simultaneous—it is incompatible with SR, and so it will not help us here.
A non-presentist endurantist had better have an answer to the NRLA. The NRLA should make us focus our attention on the definition of wholly existing at t in terms of all of an object’s proper parts existing at t. This definition has an ambiguity. It seems that either the quantification over proper parts extends over parts that exist at t, or it extends over parts existing at any time whatsoever. If the quantification is restricted to the parts that exist at t, then, as Merricks[6] notes, endurantism becomes logically trivial, it being a tautology that all the proper parts that exist at t exist at t. If, on the other hand, the quantification includes parts existing at any time whatsoever, then endurantism is incompatible with an object’s losing or gaining parts.
There is more than one way out for the non-presentist endurantist at this point. One way is to take “wholly exists” as primitive or to explicate the concept of “wholly existing” in a rather different way, say in terms of a notion of a maximal set of parts sufficient to make up that object. If one thinks with Aristotle in Metaphysics Z and with van Inwagen[7] that the true extended objects are organic, this notion might be cashed out in terms of patterns of organic interactions between parts.
Another approach requires a different restriction of quantification, and this approach is followed by Miller[8]. Instead of quantifying only over proper parts that exist at t, we quantify over all the a such that it is true at t that a is a part of o. At this point, endurantism becomes the claim that at every time t at which an object o exists, every proper part a such that o has a exists at t. This claim is non-trivial since the perdurantist thinks that it is true at any given time t that future or past time slices are parts of the object, whereas the endurantist must deny this given that the future or past time slices do not exist at t.
Any one of these three options is sufficient to respond to the NRLA. For at a time t when the cat’s tail has been destroyed, it is not true that the cat has the tail as a part. Indeed, all the parts that the cat at t has do in fact exist at t, and hence the quantification solution works. We can likewise answer the NRLA if we take “wholly existing” to be primitive. At t, the cat wholly exists without a tail. Similarly, we can say that at t, a maximal set of parts sufficient to make up that cat does exist.
Granted, in all of these responses there is a difficulty how seemingly incompatible predications could be true of an object at different times—how the self-same cat could both have a tail and not have a tail at different times. But this is simply the old Lewisian problem of temporary intrinsics. Whatever way a non-presentist eternalist uses to solve that problem should work here. Standard solutions include temporally indexing properties (being square-at-t7), including adverbial modifiers to properties (x is square t7ly; this seems to be Miller’s preferred solution), or saying that the arity of properties and relations is underestimated in ordinary language so that being square is a binary relation between an object and a time rather than a unary property of an object and having … as a part is a ternary relation between two objects and a time.
Things are somewhat more difficult for the RLA, since the notion of “a time” requires further clarification given SR. We want to be able to say that all the events happening at any one time are simultaneous, but simultaneity relations depend on the reference frame. There are two natural ways of modifying the notion of a time in a non-relativistic philosophical concept to gain a concept compatible with SR. One is to replace times with space-time points. This will not help us when we talk of an extended object wholly existing at a time, since an extended object does not wholly exist at a space-time point. The other way is to replace times with simultaneity classes so that what previously was said relative to a time t will now be said relative to the set of all space-time points that are simultaneous relative to some inertial reference frame. Such a set is known as “a space-like hyperplane”, a three-dimensional slice of space-time such that there is some inertial frame according to which all the members of the slice are simultaneous. Any given space-time point lies on an infinite number of space-like hyperplanes, since there are infinitely many inertial frames with respect to which we can definite the simultaneity class.
The endurantist who takes SR seriously should then say that an object wholly exists in every space-like hyperplane h at which it is present. This is a logical strengthening of Hales and Johnson’s definition that an object wholly exists at every time t at which it is present, since their definition is equivalent to saying that an object wholly exists at every space-like hyperplane h defined by “our” reference frame (whichever reference frame is implicit when we’re making the definition; the object’s rest frame, maybe) at which it is present. Thus, in showing the compatibility of this strengthened endurantism with SR, I will also be showing the compatibility of the logically weaker endurantism Hales and Johnson discuss.
The endurantist now needs a definition of what it means to say that an object wholly exists in space-like hyperplane h. But now the problem is no different from what we had in the case of the NRLA. We might take “wholly exists in h” as a primitive, or we might introduce the notion of maximal sufficient set of parts in h, or we might relativize having a part to a hyperplane and insist that at every space-like hyperplane h at which o exists, if o has a proper part a, then a is present in h. Granted, we will still bump up against the problem of temporary intrinsics, but the standard solutions to that problem apply just much here, as long as we replace times with space-like hyperplanes.
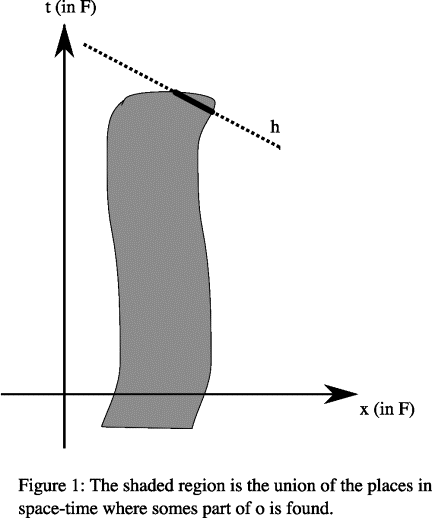
Miller herself considers a different solution, and that is to define endurantism in terms of the object’s parts being wholly present at a time relative to the object’s rest frame. Her main argument for this is that if we accept the multiple-hyperplane approach, there will be space-like hyperplanes (e.g., near the time of the object’s annihilation) which intersect the object in a relatively small portion (see the dark portion of the hyperplane h in Figure 1). We would then need to answer the difficult question of how much of an object needs to be contained in a hyperplane for that object to count as present in that hyperplane. This consideration does not, however, seem particularly strong. For that question is one that we would have to answer anyway in order to decide whether a cat that is slowly being annihilated still is present in the rest frame or has already perished.
Miller’s solution, however, runs into a serious difficulty with respect to defining the rest frame of an object. Leaving aside the difficulty of dealing with objects undergoing non-inertial motion, a difficulty that perhaps would take us into the realm of General Relativity, typical extended objects seem to consist of many parts, parts moving in different directions. My blood cells circulate—some are moving in one direction and some in another. Which parts define “the” rest frame of the object?
A natural thing to say would seem to be that the rest frame of an object is defined by its center of mass. But if a gymnast is standing on her head and moving the rest of her body, so that the center of mass moves relative to her head, why should we think that the crucial reference frame is that of the center of mass? And if she drinks some water, so her center of mass shifts, does the reference frame shift likewise?
Moreover, observe that the center of mass of an object can “move” faster than light and hence cannot be counted on to define a meaningful reference frame. To see this perhaps surprising fact, take a snake of uniform lengthwise density, stretched out along a line, so its center of mass is in its middle. Assume that the snake is 100 cm long and 1 cm wide. We then cut off 10 cm of the snake at the tail end, with a guillotine that moves at half of the speed of light. Just before we cut the tail portion, the snake’s center of mass was 50 cm from the tip of the head. After we cut off the tail portion, the snake will be 90 cm long, and its center of mass will thus be 45 cm from the tip of the head. Thus, in the amount of time that the guillotine traveled the 1 cm width of the snake, the center of mass “moved” 5 cm. But the guillotine was moving at half the speed of light. Hence, during the amount of time that the guillotine traveled 1 cm and the center of mass “moved” 5 cm, light traveled 2 cm. Thus, the average “velocity” of the center of mass over this time period was at least 2.5 times the speed of light. In fact, if the tail’s ceasing to be a part of the snake was instantaneous, then the center of mass “moved” instantaneously. Of course, the center of mass is not a real thing, and supraluminal movement of the center of mass cannot transmit a signal, and so there is no violation of physics here, just as there isn’t in the well-known phenomenon that shadows and spots of light can “move” faster than the speed of light—Reichenbach called such phenomena “unreal sequences”[9]—but the point is sufficient to show that we had better not define the rest frame in terms of the center of mass.
At the same time, intuitively, a natural thing to say would be that in the case where the object is a human being, an observer, the rest frame is the reference frame defined by the human’s sensory organs. But if the rest frame is to be defined by sensory organs, then which ones? The eyes? If so, which eye? An ear? The middle of the skull? None of these answers seem satisfactory. Once we take SR seriously, the notion of a “rest frame” of objects that gain and lose parts, or ones whose parts are in mutual motion, is a dubious one. It is much better to relativized to all space-like hyperplanes.
4. Self-intersection
Nonetheless, even though the argument has been refuted, there are surprising consequences of the view. Take two intersecting but distinct space-like hyperplanes h and k whose intersection lies within an extended object o, and suppose that o is present in h and o is present in k. Thus, we are supposing that the intersection of h and k is non-empty and some points of that intersection lie within both the spatio-temporal region that o occupies in h and the region that o occupies in k. If SR holds, and there are extended objects, this will be possible given endurantism.
Let h(o) be the spatio-temporal region of h occupied by o and let k(o) be the spatio-temporal region of k occupied by o. Then, interestingly, we see that o is wholly present in and pervades (i.e., is present at every point of) each of two different, intersecting spatio-temporal regions. The object o thus intersects itself along a two-dimensional plane (a non-empty intersection of two distinct hyperplanes will be a plane). Moreover, this oddity is not going to be a rare occurrence. It will occur in every extended object given SR and endurantism, and will occur at infinitely many places within that object.
But oddity is not impossibility, as the platypus shows. And the oddity here is consequent on the strangeness of the relativity of simultaneity which allows for two hyperplanes of simultaneity relative to different reference frames to intersect and yet contain points that are in no way (i.e., in no reference frame) simultaneous.
5. Bilocation
Consider an extended object o wholly present on each of two parallel space-like hyperplanes h and k. Suppose these two hyperplanes are very close together, and as before, let h(o) and k(o) be the space-time regions occupied by o in h and k, respectively. Then if the two hyperplanes are sufficiently close together, we can find a reference frame F, different from the reference frame defined by h and k, such that:
(a) most of the volume of h(o) consists of points p such that p is F-simultaneous with some point of k(o)
(b) most of the volume of k(o) consists of points p such that p is F-simultaneous with some point of h(o).
We can see this in Figure 1 which shows things from the point of view of F. In that figure, most of the points of h(o) (specifically, those that are above t0) are on the same vertical level as k(o), and vice versa. In the figure, being at the same vertical level indicates simultaneity in F.
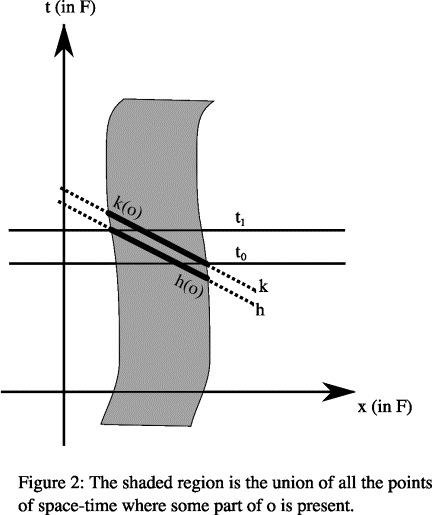
Thus, o is wholly present almost side-by-side with itself in space-time, relative to F, being wholly present in h(o) and in k(o). And once we allow an object to be wholly present in two space-time regions that are almost side-by-side, it becomes plausible that it could simply be present in two places at one time. Why not, after all? We would, granted, have to further modify the notion of being wholly present at a hyperplane into the notion of being wholly present at a subset of a hyperplane, and then we would have to employ the same solution that we had employed in response to the problem of temporary intrinsics, but now relativizing not to hyperplanes but to subsets of them.[10]
Again we at most get strangeness, but not self-contradiction. And since there are some theoretical benefits of bilocation, such as, as Koons[11] has pointed out, a neat solution to fission cases so that when a person splits into two persons she is exists in both places at once, the strangeness may overall not cost us.
6. Conclusions
Hales and Johnson’s argument against the conjunction of SR and endurantism is invalid. Making it valid requires adding a premise about the impossibility of a proper part being wholly present at more than one time, a premise that every endurantist who believes in proper parts will deny.
However, there is an interesting argument against the conjunction of SR and endurantism in the case of objects like cats that can lose parts. But this argument, it turns out, is no more pressing given relativity than without relativity, as long as we realize that times need to be generalized to space-like hyperplanes.
There are, however, some strange consequences of SR and endurantism. But in light of the strangeness of SR, this further strangeness does not appear to carry all that much evidential weight.